This Is How Data Kills Creativity
Header Photo by Chris Liverani on Unsplash
UPDATE - Sept 27, 2019
It looks the original LinkedIn article has been taken down and sadly the Wayback Machine doesn’t index LinkedIn content. And interestingly, the author, Josh Fechter, seems to have disappeared from LinkedIn completely.
I used to have an allergic reaction to the mere suggestion that data kills creativity. Over the years I've found this narrative repeatedly popping up in my newsfeed, and for the longest time I couldn't figure out why people were still discussing this. Hell, it's even a question on Quora.
My view on the topic up until about 2 years ago was simple. I staunchly believed that anyone who actually subscribed to the idea that data was the killer of all things creative was just plain nuts. Surely these people were just narrow-minded and out of touch, right?
Well the truth is plenty of people do feel this way, and I've come around to the idea. Not because I actually believe data kills creativity. But because I sympathize with why a reasonable person might think so. After all, your data is only as good as the business question you're trying to solve, and subsequently the quality and sophistication of your analysis. I see a lot of bad advice out there steering people in our industry toward either low-value or unsophisticated applications of data analytics. And I think it's the bad advice that might give some folks the wrong idea about why, how and when data should be used to make us, and the work we do, better.
The latest example of what I would consider bad advice appeared in my feed just last week. It's an article titled The One Number that Determines Whether Your Posts Go Viral on LinkedIn, and it claims to have cracked the code for understanding when content goes viral on LinkedIn. In short, the article offers a benchmark (i.e. 142 likes) as a threshold for going viral. The main idea is that if you can reach 142 views per like on your post within the first hour of it being published, then you’re on your way to 100K or even 1 million views.
My main gripe here is that the author shared the results of what looks to be an unpolished methodology and which applies some questionable math. He then reports the findings of his experiment (to his massive LinkedIn audience) and claims the results have a high degree of confidence. Sharing the findings of a work-in-progress methodology and being transparent with your readers is one thing. But sharing unproven or potentially invalid results and suggesting they're somehow statistically confident is another thing entirely.
That's dangerous.
Why?
Here's a snapshot of the almost universally positive comments on the article.
These folks all trust the data and insight that was shared. They trust that the methods and tools used to derive the "magic number" were robust, and some will probably take these insights back to their company, colleagues or clients. But the problem is, as I'm about to show you, the numbers don't add up.
I want to run through the major problems with the methodology used in the original article so we can all learn from this (the original author included). It's worth noting that I think the idea behind the experiment he was undertaking is really interesting, and it's something I hope he continues to explore and refine, just with a little more sophistication.
But for now, lets break down some of the issues.
Let's start with this quote (emphasis mine):
The number 142. That’s how many views a post will get for every Like – on average – with a 90.04% confidence.
I want to walk you through how the author arrived at these numbers. I actually commented on the article asking for some clarification on how some of the calculations were done, but didn't get a response. The good news is that the author shared access to the original dataset he used in a Google sheet, which you can access here (this is a copy I shared to my own Google Drive in case the original gets deleted). It wasn't too hard to reverse engineer as all of the functions are still intact.
One thing I'm not very clear on is where the author states that the data in the spreadsheet has been "reduced for simplicity". I honestly have no idea what this means. Either he's suggesting that he cut down the number of samples used for the calculations (i.e. articles) as the spreadsheet only includes 7 posts. But I don't think that's the case because the math (specifically the 142 benchmark) squares perfectly with the 7 posts provided. So I'm pretty sure these 7 posts reflect all the data he crunched. On the other hand, he may have meant that he removed or hid some of the variables in the spreadsheet to make it easier to read. But again, all of the variables you need to produce the same calculations are clearly laid out in the spreadsheet, so it doesn't seem like other variables are being used. So again, I don't know what the author meant when he said the dataset has been "reduced". Perhaps he'll reply to this article and clarify if I've missed something.
Anyways, moving on.
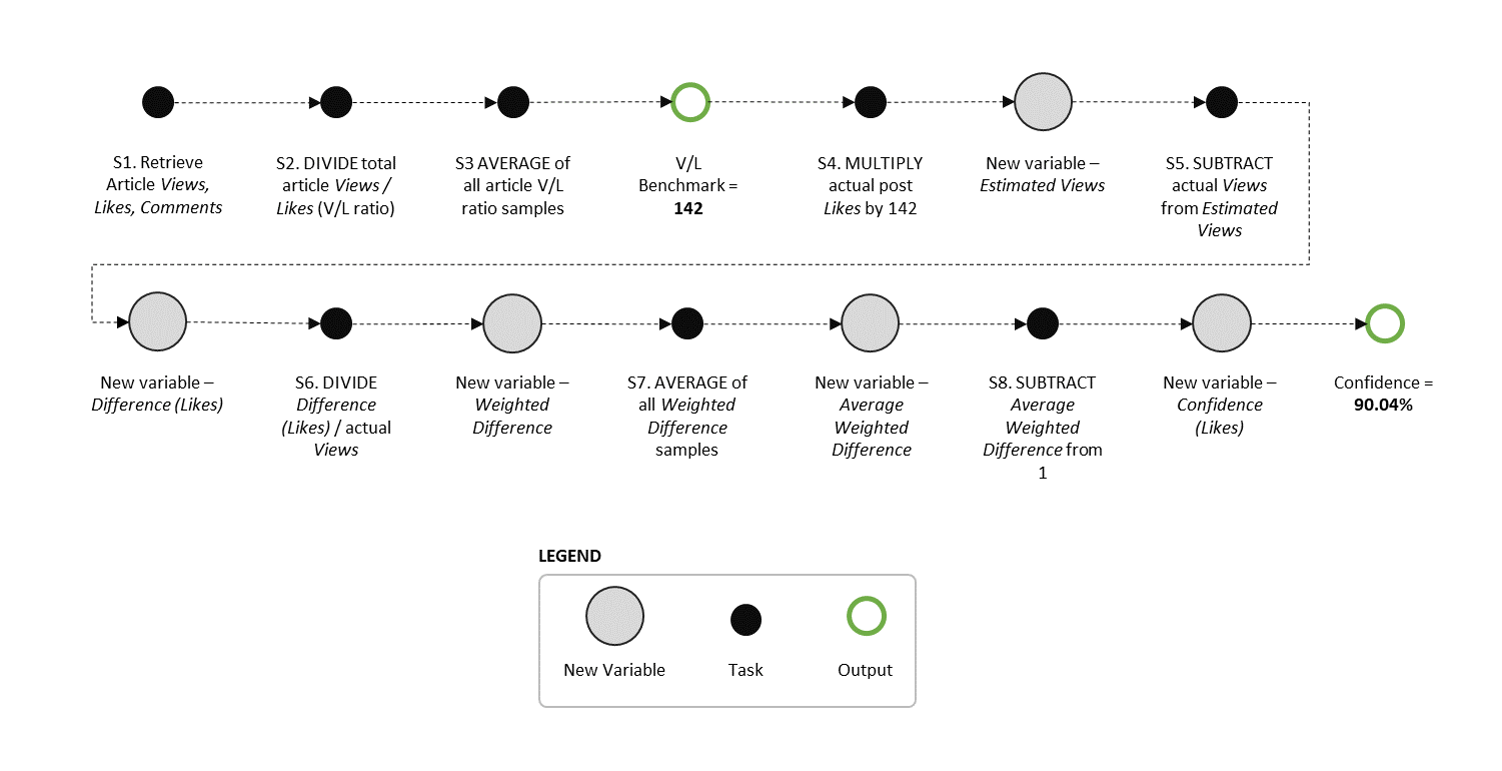
So I spent some time going through the Google Sheet and worked out both the calculations and sequence the author used, outlined in the diagram below. In case you haven't noticed, I like to model things 😝.
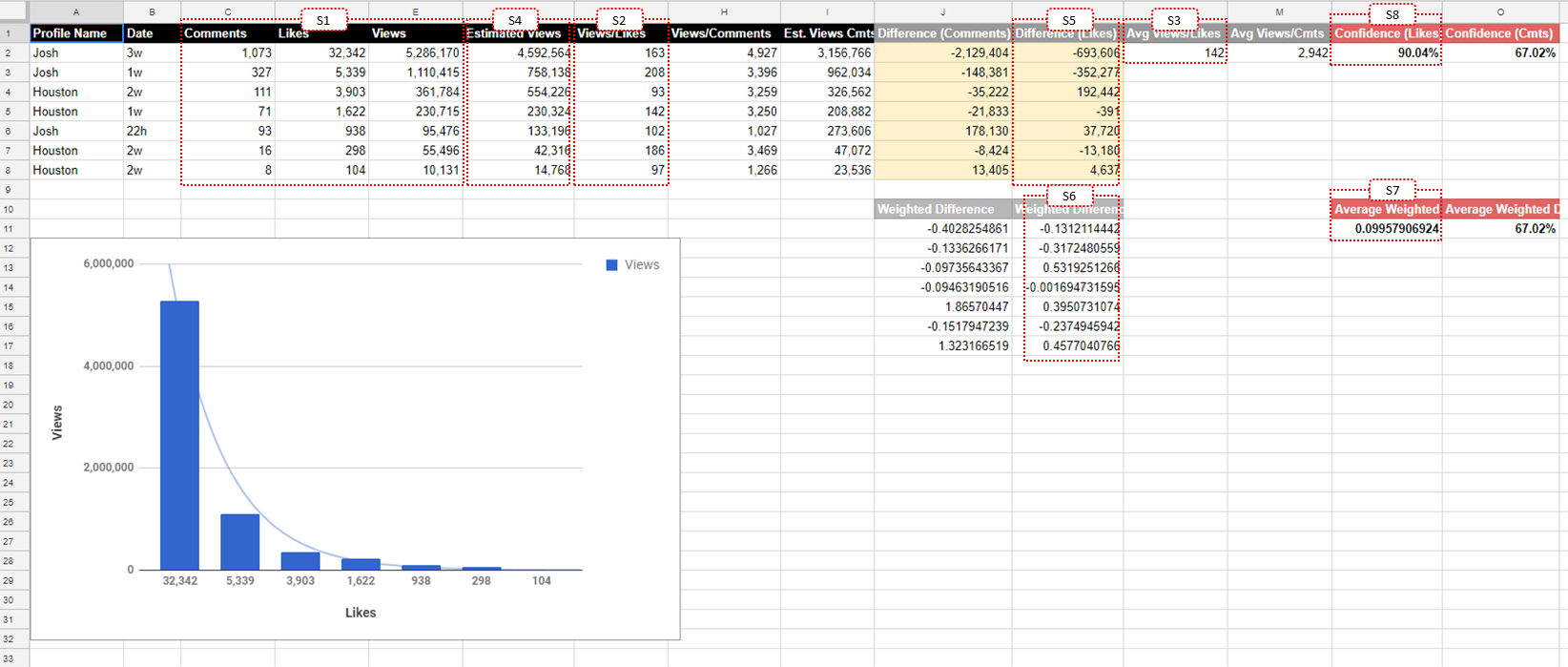
And based on the sequence, here are the steps (i.e. S1, S2, S3, etc) overlayed on the Google Sheet they shared.
Why did I go to this extent to map out his approach? Two reasons. First, it's important that we all understand what was done here, and why plugging in a few functions in Excel or Google Sheets isn't the same as running robust statistical tests. And second, it will help you understand where exactly the math goes sideways.
Just to give you a quick play-by-play of what's happening in the spreadsheet pictured above, the author starts by taking a sample of viral articles on LinkedIn and he works out the average view-to-like (V/L) ratio by dividing total article likes by total views (S2). Then he calculates the mean value for all 7 posts (S3). This produces the 142 figure he quotes early in the article. Everything that happens after this point seems to be done to validate if the 142 holds true as a benchmark for the V/L ratio among viral articles.
To validate the 142 benchmark the author multiples each of the 7 articles total likes by 142 to generate an estimated views figure (S4), and then he calculates the percentage error (not to be mistaken with percentage difference) as a way to evaluate how accurate his V/L ratio benchmark (142) is when it comes to predicting actual views. And this is where it all starts to fall apart.
Mean scores and negative values
The first critical error is that the author calculates the mean absolute percentage error (also known as MAPE) for all 7 articles without ignoring the minus sign (see S6 in the screenshot above). Why is this important? MAPE is typically used to calculate the accuracy of a forecast in statistics, but the direction of the error makes no difference (i.e. whether your estimation was above or below the actual value). So when calculating MAPE you're supposed to drop the minus sign for any negative values. If you don't do this, the negative values will drag down the mean, making your MAPE calculation worthless.
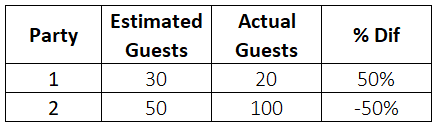
Here's an example. Let's say I'm planning to throw two birthday parties, and I estimated that 30 guests will show up to party #1 and 50 guests will show up to party #2. And then the actual attendance looks like this:
By all standards I'd be pretty terrible at estimating. But I digress.
In both of those cases I was 50% off in terms of estimating party attendance. For the first party, I overestimated by 50%, and for the 2nd party I underestimated by 50%. But like I mentioned before, the direction of the error doesn't matter. So I need only say that I was 50% off in either case. Not that I was +50% off in the first case and -50% in the second case.
If you were to calculate the mean of both cases without ignoring the minus sign, the average would be zero. Which means, on average, there was 0 error in my estimation, which we know can't be true. But if you ignore the minus sign the mean error rate is 50%, which is the correct value.
And this is exactly what the author has done, which is he didn't ignore the minus signs. When calculating the mean percentage error (see S6) he was working with 4 samples that were negative, and which should have had the minus signs removed from the calculation. Without ignoring the negative sign, this produced his estimated error rate, which was 9.96%. When in fact, the real mean error rate, or MAPE, is 23.96%. That's a huge difference.
Confidence in numbers
The second critical error the author made was with how he extends the flawed MAPE value to then calculate what he refers to as "confidence". I'll come back to what confidence actually means here in a moment, but first let's talk about the calculation.
Early in the post the author stated that his 142 V/L ratio is robust, with "a 90.04% confidence". He reminds us of this again later in the article when he states:
Our views per like ratio is 90% accurate when analyzing posts after they’re live for three days.
But how exactly did he calculate the "confidence" figure? By subtracting his MAPE value (or what he refers to as Average Weighted Difference) from 1. That 's it, 1 minus the mean error rate. Unfortunately statistical confidence doesn't work like this, especially when it comes to MAPE.
Consider this limitation of MAPE as on an example. When you underestimate a forecast the percentage error can't exceed 100%. But when it comes to overestimating there's no upper limit to the possible error (your estimate could be 10,000% above the actual). So how could subtracting your error from 1 give you any kind of indication of confidence?
What seems to be happening here is that he's assumed the inverse of his error equates to accuracy (or confidence as he puts it). So if the mean percentage error was only 10%, he's assuming that implies he's correct 90% of the time. Unfortunately, that's not how it works. He hasn't tested how often his model is correct, he's tested the average variance (or error) in his model's ability to estimate views vs the actual post views. Based on his calculations, the only true finding he can report on is that his model's mean error is 23.96% (which using his original logic means his model is only 76% "confident"). But in general, saying that the inverse of your error rate somehow demonstrates confidence in a forecast or model is wrong.
And this brings us back to what the author meant by confidence. Saying the results are 90% confident suggests to the readers that he's has run some kind of statistical test and is, in turn, reporting statistically sound findings. But the fact is the methodology used here is flawed, the findings aren’t proven, and the statement that these results are 90% confident is false.
Listen, I get what the author was trying to do here, and I know he meant well. And frankly, had he of just laid out all of the math in his article without touching the "confidence" bit I would have left this alone. But he didn't. He cited what sounded like a robust statistical outcome, which gave his methods and findings more authority with his readers. Words matter, and when you take into consideration the size of the following this article was shared with, the author has a responsibility to check his math before sharing the results. Or at the very least, if he want's to share untested results then just don't throw around terms like “confidence”. It’s totally fine to report untested findings for something that's a work in progress, just be transparent with your readers.
We need to be better at knowing our boundaries. If you have a theory that you want to test and this requires a good handle on research methods, statistics or even just basic algebra, you have a responsibility to either spend the time and acquire the knowledge you need to do it right, or find someone qualified who can help you.
A few more problems
So we've covered off the fundamental problems with the math, but there are also some issues with the overall methodology that I want to touch on. I won't go in depth here, so here's a quick-fire list of the issues:
Sample Size - The author only included 7 posts in the experiment, which isn't nearly enough. The 7 articles also vary considerably in terms of views and engagement volume, as well as engagement rate, V/L ratio, etc. Addressing the issues posed by the variance is mostly a matter of introducing more sample. So they need to crunch more posts.
Data Sources - The articles are sourced from two different authors, 4 from the actual author of the post and 3 from his co-founder. But they both have considerably different sized followings on LinkedIn (one has 34K followers while the other has 3.4K), and network size is most likely an important variable to consider.
Untested theories - The author mentions early on that most articles on LinkedIn "only go viral for 3 days". And this assumption plays a key role in some of his calculations. But he hasn't substantiated this theory in any way that I can see, so there's no way to confirm whether the benchmarks he offers (i.e. how many likes you need in the first hour) hold true. Also, it's not clear if the data for the 7 posts was pulled at exactly the 3 day mark (as it would need to be based on his assumptions). This is questionable given the Date column in the shared Google Sheet lists one of the posts as 22h (does that mean it was extracted after only 22 hours?).
Accounting for velocity - The author assumes that the average viral LinkedIn post life-cycle lasts 3 days, but he hasn't properly accounted for or measured the velocity of engagement over more granular time intervals, particularly the first few hours of publishing an article. And this is a BIG problem as the whole experiment is based on predicting early signs of virality. Notably, when estimating how many likes a post with 1 million views needs to receive in the first hour, the author arbitrarily weights down his benchmark from 97.8 likes to 50-60 likes to try and account for the potential difference in velocity in the early hours vs latter hours of being published. But this isn't based on any hard numbers.
Some closing thoughts
Like I said at the beginning of this post, I actually think this was a really interesting idea and I really hope the author continues to explore it further and refine his methods. And there's plenty of great resources on LinkedIn to do this. In fact, here are a few relevant LinkedIn groups that the author could potentially leverage to share, discuss, and expand the methodology:
Data Mining, Statistics, Big Data, Data Visualization, and Data Science
Research, Methodology, and Statistics in the Social Sciences
But I do have one last comment I wanted to make about the underlying message here, which stems from this quote where the author was making a statement about his general approach to publishing on LinkedIn (emphasis mine):
We know when we’ve hit virality to the point where if posts are not getting strong enough engagement, then we take them down.
Here's the thing, is this really the message we want to be sending, especially in the name of data? I love writing and think everyone should do it. And if I'm being honest, I never feel like I've fully thought something through until I've written about it. I'm proud of every article I hit publish on, whether on LinkedIn, Medium, my blog or somewhere else. Sure, some of my articles are better than others, but I'm still proud of them. Because each and every article I write is a learning experience, and I grow as a result.
And the idea of simply deleting something because it doesn't get enough likes is pretty crappy advice if you ask me. Look, I get the article was primarily targeted to content marketing for brands, and in that specific context then maybe this is all fine. But the lines between personal and corporate branding are blurring as we see more and more people starting to share their ideas on platforms like LinkedIn. And I feel like we should be encouraging people to care about what they write. I guess what I'm saying is you should write for yourself first and foremost, not for your audience. And certainly not just for views, likes or engagement.
This advice goes against every content marketer’s 'top tips' for creating engaging content. Because they all say to write for your audience. And if you're a soulless brand with an army of ghostwriters, then fine, write about what's trending on Twitter. But if you write for yourself and what you're passionate about, you might end up starting a trend or two.
So please, think twice about deleting content just because it doesn't get you the numbers. And don't always take the findings of an experiment you read about online at face value.
And as far as data-driven content marketing goes, I think we can find better uses of data. So let's focus our efforts on the more meaningful, actionable and impactful applications that make us smarter and, perhaps, even a little more creative.
Thanks for reading.